The likelihood of someone guessing a 4-digit PIN correctly on the first try is 1 in 10,000 (or 0.0001), but this assumes a completely random distribution; in reality, some PINs are much more common, increasing the likelihood of a successful guess. [1, 2, 3, 4]
Here’s a more detailed breakdown: [1, 2, 5]

• Possible Combinations: For a 4-digit PIN using numbers 0-9, there are 10,000 possible combinations (10 x 10 x 10 x 10). [1, 2, 5]
• First Attempt Probability: Therefore, the theoretical probability of guessing the correct PIN on the first try is 1/10,000. [1, 2]
• Real-World Scenarios: However, people often choose predictable or easily remembered PINs, such as: [1, 3]
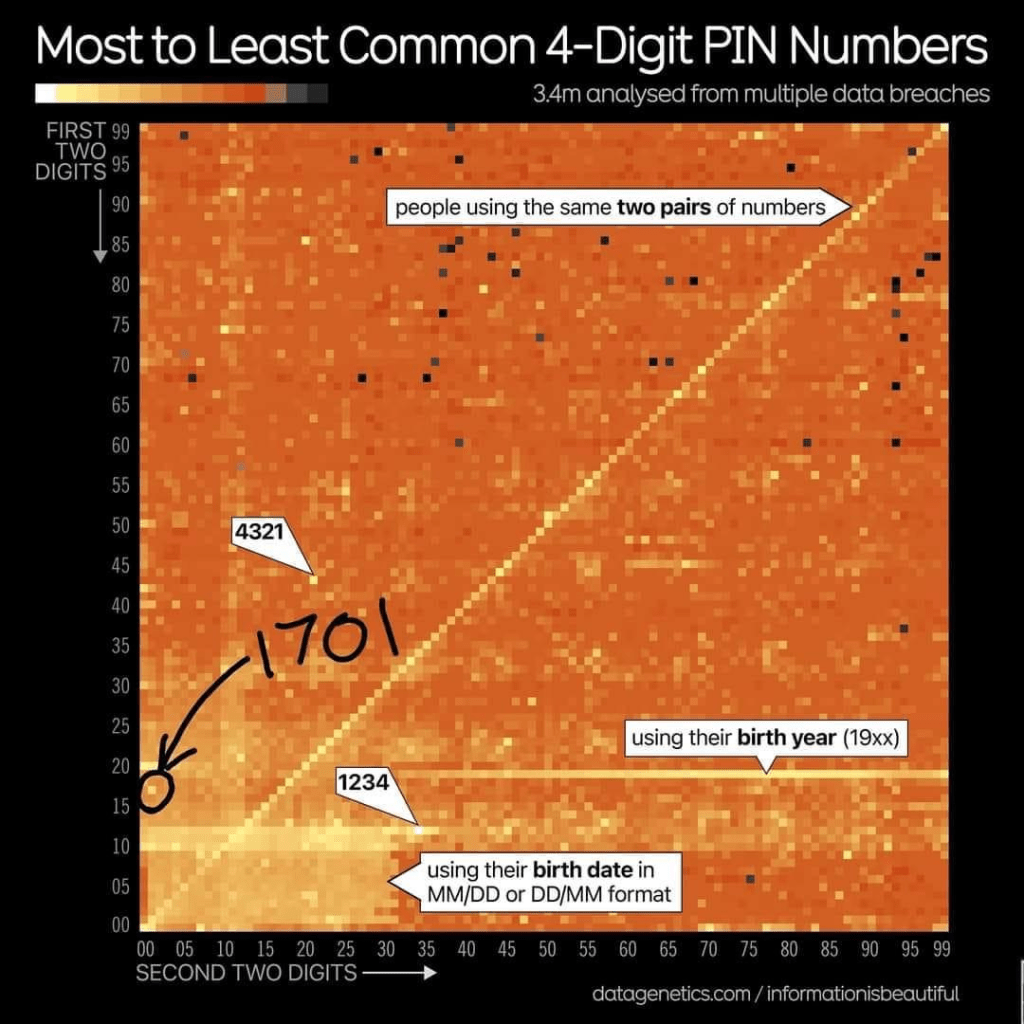
  • 1234, 1111, and 0000 are very common, making them easier to guess. [1, 3]
  • Studies have shown that these 3 numbers represent almost 20% of 4 digit-codes samples taken [1]
• Common Trends: Other common PIN patterns include repeating digits (e.g., 1111, 2222), sequential numbers (e.g., 1234, 2345), or numbers related to birthdays or anniversaries. [1, 3]
• Implications: The likelihood of someone guessing a PIN successfully depends heavily on how random the user’s chosen PIN is and also if they use common PINs. [1, 3, 6]

Generative AI is experimental.

[1] https://www.quora.com/What-are-the-odds-of-someone-guessing-a-person-s-six-digit-PIN%5B2%5D https://homework.study.com/explanation/most-atm-cards-require-a-4-digit-pin-number-the-chances-of-a-person-guessing-a-pin-number-on-a-single-attempt-the-answer-is-1-in-5-040-but-what-is-the-process-of-getting-5-040.html%5B3%5D https://wired.me/technology/security/1234-might-just-be-the-reason-you-get-hacked/%5B4%5D https://www.quora.com/What-is-the-probability-of-getting-a-four-digit-PIN-number-that-starts-with-5%5B5%5D https://www.theamegroup.com/uncategorized/how-do-i-create-a-strong-pin/%5B6%5D https://www.cio.com/article/296766/security0-atm-pin-numbers-easier-to-steal-than-you-think.html

Going to revisit, the math…. look at it for the time being…

trying to get in a building…

0911 and the rest… guess away…